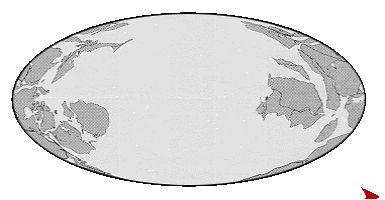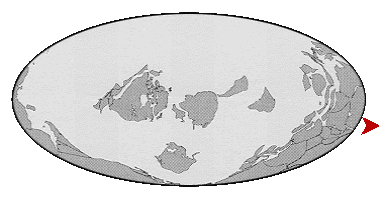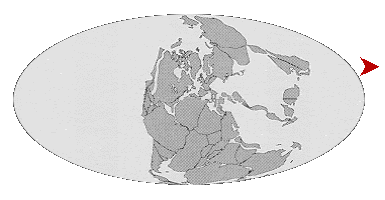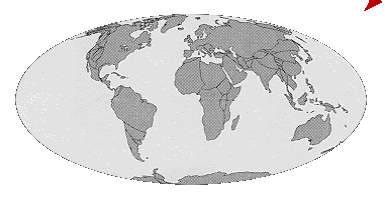
Excellent discussion
-
Recent Posts
Archives
Categories
- Africa Keystone of Pangea
- American Canyon Earthquake
- Animal Behavior
- Anthropic interglacial
- Anthropocene
- Anthropology
- Asteroid Impacts
- Asthenia
- Beggaring Science
- Biology
- Body Language
- California Drought
- Carbon Cycle
- Carbon Dioxide Loves to Swim
- Carbon Prohibitionists
- Carbon Theology
- CERES
- Chaos
- Climate
- Climate and Civilization
- Climate Change
- climate sensitivity
- Cold is the New Hot
- Continental Wander Path
- Cretaceous normal superchron
- Dud PDO
- Ecology
- Economics
- Energy Budget
- Energy of Photons
- ENSO
- Ethics
- Extinctions
- Fourth Law of Thermodynamics
- Geography
- Geoid
- Geological Evolution of the Western United States
- Geology
- Global Mean Sea Level
- Global Warming
- Global Warming Denial
- God and Dice
- god of chaos
- Government Industry
- Grand Canyon
- Gravity Anomalies
- Gravity Potato
- GRBaV
- Greenhouse Effect
- Greenhouse Spectra
- Half Dome
- hard data
- Having one's head up one's maths
- History
- History of Life
- Hold and Haul
- Holocene
- Human need for Judgdment
- Isotope Integrated Carbon Cycle
- Judge Alsup Questions
- Large Igneous Provinces
- LLSVP
- LLSVP's are Doughboys
- Magnetic Reversals
- Manual Prayer
- Metaphor
- Microbial Dark Matter
- MODTRAN
- Moho
- Mount Whitney
- Ocean Acidification
- Oceanography
- Optical Material Properties
- Pacific Triangle
- Paleo Sea Level
- Paleoclimate
- Paleogeography
- Pandemic
- PDA and the Apple of Eden
- PDO
- Photon
- Photon Food Fight
- Physics
- Plasma
- Plate Tectonics
- Pressure Broadening
- Radiance
- Randomness
- Red Blotch Disease
- Relationship of SST and 200hPa Anomalies
- Religion
- RGBaV
- River
- Rocks
- Salvation from Cows
- San Francisco Rainfall
- SARS 2
- Seafloor Isochrons
- Seamount Chains as Incipient Island Arcs
- Seismic Tomography
- Serpentine
- Shamanism
- Sheepherders and ignoramuses
- Sierra View
- Sociology
- Solar EUV
- Spectra
- Sustainability
- the "Pause"
- True Polar Wander
- Unsaturated "black hole" H2O bands
- Virtual Geomagnetic Pole (VGP)
- What's going on here?
- Wilderness
- Wine
Meta